Statistical significance
Statistical significance means the effect of a treatment or the difference between parameters compared is adequately big and that it is unlikely due to chance. For many statistical analyses such as t tests and ANOVA, statistical significance is indicated by the p-value.
The p-value
A p-value that is lower than a pre-determined significance level called alpha (alpha = 0.05 is commonly used) means the difference is statistically significant. However, it is possible to have a statistically significant outcome for a very trivial effect or small difference when sample size is very large and when sample variability is very low.
Practical significance
Practical significance means that the effect or difference is meaningful in real life.
An Example
To elucidate the difference between statistical and practical significance, we’ll look at an example. Let’s compare the home team average goals per game and the visiting team average goals per game in the National Hockey League (NHL) for the last 5 years (2018-2019 season stats). Using Welch’s 2-sample t-test, below are the results.

The p-value is less than 0.05, which means that the difference is statistically significant. The following is a plot of the means with 95% confidence intervals. They do not overlap which confirms our conclusion that statistically there is a difference between number of goals scored at home versus away.
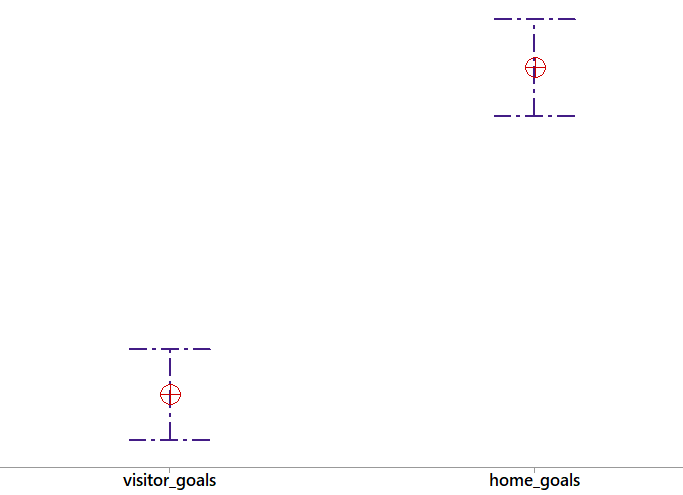
But hold on.
There is information missing here. Notice the estimated difference is +0.2741 goals in favor of home team (with a 95% Confidence Interval of +0.2181 to +0.3301). In real life, the difference is negligible since the it is less than 1 (in hockey goals are whole numbers and not decimal numbers).
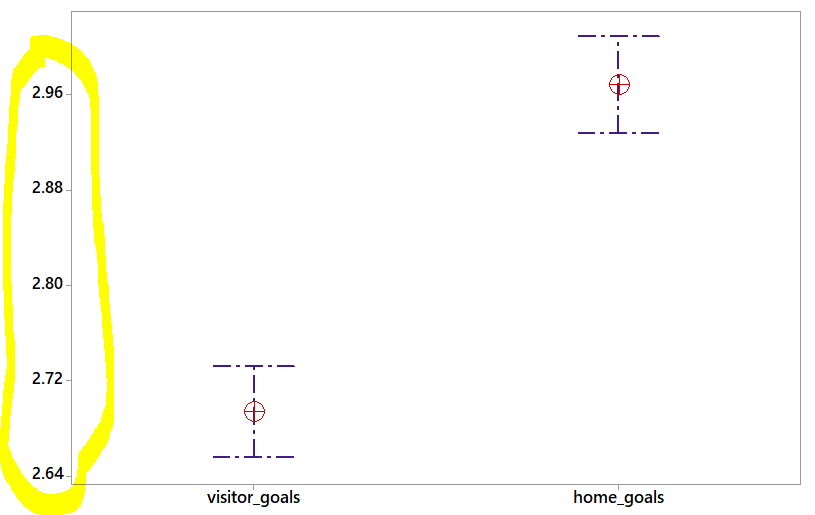
Practical Significance
The large sample size (6,670) likely contributed in producing a statistically significant difference. Practically, there is no difference between the average goals of home and visiting team. It is an important distinction to make!
Special Contribution
Special thanks to contributor Raul Rosal. Raul is a Lean Six Sigma Master Black Belt
and APICS Certified Supply Chain Professional. He is currently pursuing his Masters of Applied Statistics from Penn State University.